Mathematician Ruth Haas works on mathematical models and in particular the study of counting, which is called combinatorics. She revels in the quintessential problems and constructs of mathematical research, where reality meets abstraction and chaos meets order and ultimately offers new pathways to understanding the world.
/ Published December 6, 2013
As a theoretical mathematician specializing in combinatorics, Ruth Haas explores the deep underlying principles of mathematics that influence how the world we inhabit is organized. The professor of mathematics and statistics and of engineering at Smith conducts research that is both algebraic and combinatorial, spanning both theoretical and applied topics including combinatorics, splines, commutative and computer algebras and operations research. Accordingly, the thinking she engages in uses permutations, abstract algebra and graph theory to understand patterns and highly abstract structures. Haas was recently appointed to a chaired professorship, and her inaugural lecture as the Achilles Professor was titled “Reconfiguration.”
Afterwards she spoke with Insight about her research, including her reflections on the investigations mathematicians are motivated to pursue.
Q. What is combinatorics?
A. Combinatorics is a broad field closely aligned with computer science. It is the study of counting. It comes from the word “combination.” In combinatorics there are two basic questions: How many are there? (which is counting) and What are they? (which is enumeration). Say you invite six friends for dinner and you want to know how many different ways you can seat them around the table. How many combinations are there? Or let’s say you have 10 friends and you have three tables of three and there is somebody you are not going to invite. How many ways can you divide them up? We could then ask for other properties, such as which arrangements seat couples together? A permutation is a rearrangement of a set. While permutations around the dinner table are not deeply important, there are many more serious applications.
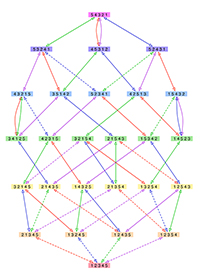
The reconfiguration diagram for involutions on five elements under the reconfiguration rule that allows only switching two neighboring elements. An involution is a permutation, which when done twice results in the original order. Click to enlarge.
Q. So what do you mean by “reconfiguration”?
A. This describes moving from one good solution to another good solution, and it raises almost limitless questions. How many steps might it take, for example, to go from one acceptable seating arrangement to another if we introduce a rule that in each step only two people sitting next to each other can change places? What is the least number of permutations you have to pass through? Is there more than one way to reach the same outcome? If so, how many? Can you get from a particular solution to any other? Reconfiguration means you have a bunch of solutions and some rule for how you are allowed to move from solution to solution.
Q. What do you learn from spinning out problems like this?
A. It sounds trivial when phrased in terms of the dinner table problem. In fact, understanding how permutations work is understanding how objects move in space, how symmetry works, how chemistry works. The remarkable thing about combinatorial mathematics is that you feel like you are just playing games, but in fact the patterns that come out of these problems turn out to explain complex mathematical and physical structures that are important to all of us—whether we realize it or not. They illuminate a lot of deep, underlying mathematics.
Q. Tell us more about that.
A. Mathematics is about creating and understanding abstract models of reality. The goal of abstract mathematics is to explore and understand the abstract models.
Q. What is a problem you are working on now?
A. I am doing something called “domination in graphs.” A graph is a set of vertices with edges between them. Imagine city streets with corners at the intersections. Think of domination as putting police officers at the intersections so that they can see down every street there is. A dominating set is a set of “officers” at some vertices that can see everywhere. The reconfiguration problem is very practical because individual officers change, they go on and off duty. If you put a new officer at a new intersection so an old one can leave, how do you accomplish this without leaving anything uncovered at any point? That’s the idea of reconfiguration in domination.
Q. Are the constructs you work with related to things you would find in nature?
A. Related yes, but perhaps not directly. Applied mathematicians have a more direct relationship with reality. A colleague in math biology works with a biologist who will say “here’s what I see with snails and crabs; can you help me make a model that explains this phenomena?” Theoretical mathematicians take applied models and abstract them even further. We try to push them to understand the limits. We get pretty far away from readily perceived reality. It’s very abstract.
Q. How do mathematicians decide which abstractions to investigate?
A. We are motivated by trying to figure out as much truth as possible. The broad goal is to understand everything about everything. The way to make progress toward that is to figure out what question there is that you might actually be able to get an answer to in mathematics. Framing the question, even knowing what to ask about how something works, can be a very difficult thing. You don’t know how something is going to work until you know how it works—and if you already know how it works then you wouldn’t have to study it. You often ask one question and end up answering a different one. That’s the nature of mathematical research.
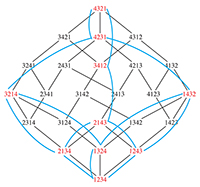
The reconfiguration diagram for involutions (in red and blue) is superimposed on the diagram for all permutations on four elements. Click to enlarge.
Q. Are there always words to describe the questions you are asking?
A. I was working with some students today who had to invent their own language to advance their project. A striking thing about my branch of mathematics is that many of the names sound made up because, well, we make them up. We have things called a “matroid” and a “greedoid.” In graph theory there is something called a “tree,” a “flower,” a “forest.”
Q. What is unusual about those names and what do they signify?
A. There is nothing unusual about these names. They just seem funny to a non-mathematician because they are words we use in daily life, and people expect math words to be different. The particular words I mentioned here signify graph structures that look like a tree, flower or forest.
Q. If you publish an article do the names you invent become part of the nomenclature?
A. In a new field, sometimes things have multiple names. Somebody will call something a “path,” somebody else will call it a “walk,” and somebody else will call it a “trail.” It may take 40 years until the language gets standardized and everybody refers to things by the same name.
Q. Do you bring computers to bear on patterns you are trying to decipher?
A. More and more. You have this machine on your desk that will do computations in a few seconds and will generate visualizations of the patterns in your data. Even seven years ago, when I started working on involutions, for example, we had problems that would crash the machine. Now you can do them in 10 minutes. A lot of what I do is to figure out how to get computers to understand what it is I want to talk about.
Q. What is the relationship between computer science and combinatorics?
A. Computers are based on binary arithmetic. They are possible because we’ve figured out how to turn switches on and off to represent zeros and ones. That’s a discrete thing, so that’s combinatorial. Computers and combinatorics have grown up together. Combinatorics made computers possible. At the same time, because of computers we can now solve more combinatorial questions, so there’s a back-and-forth.
Q. Is asking you to describe the practical applications of this research a valid question?
A. It is and it isn’t. I don’t use that as a day-to-day motivation. I’m not going to cure cancer. I’m not going to make cell phones work better than they do. It’s the nature of humans to explore. We have art, we have music and we have philosophy. We do many things that don’t directly make us more money or make us healthier, but they increase our understanding of the world. Even crazy theoretical mathematics that people have created over time turns out to be applicable. Things that seem like purely fun games, pie-in-the-sky mathematics when they were developed a hundred years ago, now turn out to be useful models—not all of it, but a lot of it.
Q. That speaks to the fact that there is a logic to the world that we live in.
A. That’s right. I think it is human nature to try to understand that logic.
Q. Where is this heading?
A. Now you are getting to a philosophical question. Mathematics gives us abstract models to address complex, real-world problems. The nature of humans is to play with structures and create new things and to see where paths lead. There is always new stuff to explore and new variations to consider. Further, there is an aesthetic. The human mind appreciates patterns, whether they are symmetrical patterns, or other kinds of patterns whenever they show up. We appreciate seeing order out of chaos.
Ruth Haas, who has been instrumental in the establishment and implementation of the prize-winning Smith College Center for Women in Mathematics, believes that nobody should be intimidated by math. “I teach a great variety of courses, and most of my students are not going to be mathematicians,” she says. “But I want them to feel comfortable with it and to know it is not this big scary thing; it is like using a different language.”
She came to Smith almost 25 years ago because she wanted to be at an institution that values teaching as well as research. Over the years, she has developed a reputation not only as an educator who encourages non-math majors to engage with a subject many people avoid, but also as a mentor to students who want to make a career of it.
Haas doesn’t minimize the fact that “math is inherently hard,” but then again “everything becomes hard sooner or later,” she says. Learning that they can overcome obstacles not only gives students a sense of confidence, but it puts a tool at their disposal that will be valuable in whatever they do later in life. At its core, she says, the discipline is about learning how to think abstractly.
Her role in encouraging advanced students is slightly different. For many of them, she is a trusted adviser they come back to, sometimes years after graduating from Smith, to seek counsel on navigating the thickets of a field that traditionally hasn’t welcomed women. Haas has been remarkably successful in promoting former students, many of whom she first engaged with as co-director of the Center for Women in Mathematics, which she helped found seven years ago. It is a one-year post-baccalaureate program for women contemplating becoming professional mathematicians.
Her colleague, James M. Henle, the Myra M. Sampson Professor in the Department of Mathematics and Statistics, says Haas “pours her energy” into her mentoring. The result, he says, is her “astonishing success” at “turning doubtful, unconfident, tentative, conflicted young women into mature, confident, successful mathematicians.”
Henle notes that of the U.S. women earning doctorates last year in the subject at the top 100 schools in the nation, “over 7 percent of them were mentored by Ruth Haas.”
Haas describes her mentoring work in part as letting young people know that everybody who reaches a high level in the field has gone through bouts of failure and self-doubt. She introduces students to a variety of people working in the field. “They see somebody older and in a nice position, and they assume we always knew what we were doing and it all went well all the time—and so just to see us talk about the road bumps we hit along the way is very useful,” she says.
Haas also makes it her business to stay current with what is going on in graduate programs around the country. If a student is interested in a particular program “I can say, ‘call or email this former student; she’s there now and can give you the inside scoop’.”
Mentoring “is just about having a personal connection with the students,” says Haas. “I don’t mean getting involved in their personal lives, but getting them to realize their potential.”
